- Auteur Matthew Elmers [email protected].
- Public 2024-01-11 06:59.
- Dernière modifié 2025-01-24 09:24.
Dans cet article, nous essaierons de comprendre la pénétration du blindage des canons des cuirassés Bayern, Rivenge et Pennsylvania, ainsi que la qualité comparative des blindages allemands, américains et britanniques. C'est extrêmement difficile à faire, car les données sur les canons américains de 356 mm, allemands de 380 mm et britanniques de 381 mm sont très sommaires et incomplètes, et se contredisent parfois, mais nous essaierons quand même.
Quel est le problème exactement? Voyons comment la plupart des fans de l'histoire navale (et pas seulement) comparent la pénétration du blindage de certaines armes. Par exemple: dans une publication consacrée, par exemple, aux cuirassés anglais, il y a des informations selon lesquelles un projectile britannique de 381 mm de la Première Guerre mondiale a percé une plaque de blindage de 381 mm à une distance d'environ 70 câbles. Dans une autre édition, consacrée aux navires « capitaux » déjà allemands - qu'un projectile allemand similaire de 380 mm « maîtrisait » un blindage de 350 mm avec seulement 67, 5 câbles. Il semble en résulter que le canon anglais est plus puissant - c'est précisément la conclusion qu'on en tire.
Cependant, en réalité, comparer des données comme celle-ci de cette manière est très facile à mettre dans le pétrin.
Les données ci-dessus sont-elles obtenues à la suite d'un tir réel ou sont-elles calculées à l'aide de techniques de pénétration du blindage ? S'il s'agit des résultats d'un tir réel, les conditions étaient-elles identiques pour les deux canons ? Si la pénétration du blindage a été obtenue par calcul, les mêmes méthodes ont-elles été utilisées ? Les données obtenues sont-elles le résultat du travail de spécialistes des ministères et départements concernés, ou sont-elles le résultat de calculs d'historiens qui ont utilisé une calculatrice ? Il est clair que dans le second cas la précision sera bien moindre… Il ne faut pas aller loin pour les exemples: prenons la célèbre monographie de S. Vinogradov, " Superdreadnoughts du Second Reich " Bayern " et " Baden " ". Dans l'annexe n° 2, l'historien respecté, avec V. L. Kofman fait un grand nombre de calculs afin de comparer les capacités des cuirassés Rivenge et Bayern. Mais hélas, il suffit de regarder le tableau des paramètres des canons de 15 pouces (p. 124) et nous verrons que, selon les calculs d'auteurs respectés, un canon anglais de 381 mm avec un angle d'élévation de 20, 25 degrés a une portée de seulement 105 câbles, soit environ 19, 5 000 m. Alors que les sources étrangères pour la même vitesse initiale (732 m / s) et un angle d'élévation légèrement inférieur (20 degrés) donnent des distances nettement plus grandes - 21, 3-21, 7 000 m. Bien entendu, cependant, de tels écarts par rapport aux valeurs réelles ont l'effet le plus négatif sur les résultats du calcul.
Mais même si les sources présentent les résultats de calculs de spécialistes, dont l'exactitude ne fait aucun doute, un autre facteur qui complique la comparaison se pose: il s'agit ici de la qualité des blindages. Il est clair que les mêmes Britanniques, lors du calcul de la pénétration du blindage lors de la conception d'un cuirassé particulier, ont utilisé les indicateurs correspondants du blindage britannique, les Allemands - respectivement, Allemands, etc. Et l'armure de différents pays peut différer en termes de durabilité, mais c'est toujours la moitié du problème: après tout, dans un seul pays, la même armure Krupp était constamment améliorée. Ainsi, il s'avère que les calculs des systèmes d'artillerie, effectués, par exemple, en Angleterre, et apparemment pour le même blindage Krupp, mais effectués à des moments différents, peuvent s'avérer incomparables. Et si l'on ajoute à cela l'absence quasi totale de travail sérieux sur l'évolution de l'étui blindé dans divers pays du monde…
En général, une comparaison plus ou moins fiable de la pénétration du blindage n'est pas une tâche aussi simple qu'il y paraît à première vue. Et, à l'amiable, un profane (qui est sans doute l'auteur de cet article) a intérêt à ne pas se saisir de cette affaire. Mais, hélas - à notre profond regret, les pros ne sont en quelque sorte pas pressés de traiter ces problèmes, alors … comme on dit, en l'absence de papier timbré, nous écrivons en texte brut.
Bien entendu, il n'est plus possible de réaliser des tests grandeur nature des systèmes d'artillerie susmentionnés, notre destin est donc aux calculs. Et si tel est le cas, il est nécessaire de dire au moins quelques mots sur les formules de pénétration de l'armure. Si des méthodes de calcul modernes sont publiées, alors uniquement dans des éditions fermées et dans la littérature populaire, la formule de Jacob de Marr est généralement donnée. Il est intéressant de noter que le professeur de l'Académie navale L. G. Gontcharov, dans son manuel d'artillerie de 1932, l'appelait la formule de Jacob de Marr. Cette formule, avec beaucoup d'autres, était répandue au début du siècle dernier et, je dois dire, elle est assez précise - peut-être même est-elle la plus exacte parmi les formules similaires de ces années-là.
Sa particularité réside dans le fait qu'il n'est pas physique, c'est-à-dire qu'il ne s'agit pas d'une description mathématique de processus physiques. La formule de De Marr est empirique, elle reflète les résultats de bombardements expérimentaux de blindage fer et acier-fer. Malgré cette "nature non scientifique", la formule de de Marr a montré une meilleure approximation des résultats réels du tir et sur l'armure Krupp que d'autres formules courantes, et nous l'utiliserons donc pour les calculs.
Les personnes intéressées trouveront cette formule dans l'annexe à cet article, mais il n'est pas nécessaire de forcer tous ceux qui lisent ce document à le comprendre - ce n'est pas nécessaire pour comprendre les conclusions de l'article. Notons seulement que le calcul utilise des concepts très simples et familiers à tous ceux qui s'intéressent à l'histoire des flottes militaires. Il s'agit de la masse et du calibre du projectile, de l'épaisseur du blindage, de l'angle auquel le projectile heurte le blindage, ainsi que de la vitesse du projectile lorsqu'il heurte la plaque de blindage. Cependant, de Marr, bien sûr, ne pouvait pas se limiter aux paramètres ci-dessus. Après tout, la pénétration d'un projectile dépend non seulement de son calibre et de sa masse, mais aussi, dans une certaine mesure, de sa forme et de la qualité de l'acier dont il est fait. Et l'épaisseur de la plaque de blindage, que le projectile est capable de surmonter, dépend bien entendu non seulement des performances du projectile, mais également de la qualité du blindage. Par conséquent, de Marr a introduit un coefficient spécial dans la formule, qui, en fait, est conçu pour prendre en compte les qualités indiquées d'un blindage et d'un projectile. Ce coefficient augmente avec une augmentation de la qualité du blindage et diminue avec une détérioration de la forme et de la qualité du projectile.
En fait, la principale difficulté à comparer les systèmes d'artillerie de différents pays est précisément « repose » sur ce même coefficient, que nous appellerons simplement à l'avenir (K). Nous devrons le trouver pour chacun des outils ci-dessus - si, bien sûr, nous voulons obtenir un résultat quelque peu correct.
Prenons donc d'abord des données assez répandues sur la pénétration du blindage du canon allemand de 380 mm / 45 "Bayern", selon lesquelles le canon à une distance de 12 500 m (ces mêmes 67,5 câbles) pourrait pénétrer 350 mm de armure. Nous utilisons un calculateur balistique pour trouver les paramètres d'un projectile de 750 kg, avec une vitesse initiale de 800 m/s au moment de l'impact sur le blindage: il s'avère qu'un tel projectile va toucher une plaque de blindage positionnée strictement verticalement à un angle de 10, 39 degrés, avec une vitesse de 505, 8 m/sec. Un petit avertissement - ci-après, lorsque nous parlons de l'angle d'impact du projectile, nous entendons ce que l'on appelle "l'angle par rapport à la normale". "Normal" est lorsque le projectile frappe le bonneplite strictement perpendiculairement à sa surface, c'est-à-dire à un angle de 90 degrés. En conséquence, le projectile a frappé à un angle de 10 degrés.de la normale signifie qu'il a heurté la dalle à un angle de 80 degrés. à sa surface, s'écartant de la "référence" 90 degrés. de 10 degrés.
Mais revenons à la pénétration de blindage du canon allemand. Le coefficient (K) dans ce cas sera approximativement (arrondi à l'entier le plus proche) égal à 2 083 - cette valeur doit être considérée comme tout à fait normale pour les blindés de l'époque de la Première Guerre mondiale. Mais ici, un problème se pose: le fait est que la source des données sur la pénétration du blindage est le livre "German Capital Ships of World War Two", où le canon 380-mm / 45 du Bayern a été comparé au calibre principal du cuirassé "Bismarck". Et ne se pourrait-il pas que le calcul ait pris en compte les indicateurs du blindage Krupp, créé dans l'entre-deux-guerres, qui était bien plus solide que celui qui était installé sur le Bayenne, Rivenge et Pennsylvanie ? De plus, l'encyclopédie électronique navweaps rapporte qu'il existe des preuves qu'à une distance de 20 000 m, des obus allemands de 380 mm ont pu pénétrer une plaque de blindage de 336 mm, et nous parlons de blindage de l'époque de la Première Guerre mondiale.
Eh bien, nous pensons: à 20 km, l'angle d'incidence sera de 23,9 degrés, la vitesse du projectile sur le blindage est de 410,9 m / s et le coefficient (K) - certains malheureux 1618, qui ne rentrent pas dans le blindage valeurs de résistance à toutes les époques de la Première Guerre mondiale. Un résultat similaire rapproche généralement le blindage Krupp de fabrication allemande d'une résistance de blindage homogène … De toute évidence, les données de navweaps contiennent une sorte d'erreur.
Essayons alors d'utiliser une autre source d'information. Jusqu'à présent, nous avons utilisé les données calculées, et maintenant nous allons essayer de les comparer avec les résultats d'essais réels du canon allemand 380-mm/45: ceux-ci sont donnés par S. Vinogradov dans la monographie précitée consacrée à l'allemand. cuirassés.
Il décrit les conséquences de 3 tirs de projectiles perforants, contre des plaques de blindage d'une épaisseur de 200, 290 et 450 mm, cette dernière étant la plus intéressante pour nous: un projectile pesant 734 kg a touché la plaque de blindage sous un angle de 0 (c'est-à-dire à 90 degrés par rapport à la surface) et à une vitesse de 551 m / s perforé 450 mm à travers la dalle. Un résultat similaire correspond au coefficient (K) 1 913, mais, en fait, il sera légèrement inférieur, car les Allemands ont trouvé leur projectile jusqu'à 2 530 m derrière l'obstacle qu'il a percé, et - en général. Hélas, n'ayant aucune donnée sur la quantité de cette distance parcourue par le projectile dans les airs, sur la quantité de "roulé" au sol, il est absolument impossible de déterminer l'énergie stockée par celui-ci après la pénétration du blindage.
Prenons maintenant le système d'artillerie britannique 381 mm / 42. Hélas, les données sur sa pénétration de blindage sont assez vagues: par exemple, V. L. Kofman, il est fait mention du fait que ces canons britanniques ont percé un blindage de l'épaisseur de leur propre calibre à une distance d'environ 70 câbles. Mais avec quel projectile et avec quelle vitesse initiale ? Compte tenu du fait que la référence est contenue dans la monographie consacrée au croiseur de bataille "Hood", et fait référence à la période de création de ce navire, on peut supposer qu'il s'agit d'un obus de 871 kg. Cependant, une autre question se pose ici: la vitesse initiale officielle d'un tel projectile était de 752 m/s, mais certains calculs des Britanniques ont été effectués à une vitesse inférieure de 732 m/s, alors quelle valeur faut-il retenir ? Cependant, quelle que soit la vitesse indiquée, le coefficient (K) fluctuera entre 1 983 et 2 048, ce qui est supérieur à ce que nous avons calculé pour la valeur (K) du canon allemand. On peut supposer que cela parle de la supériorité de la qualité du blindage britannique par rapport au blindage allemand… ou est-ce que la forme géométrique du projectile allemand était mieux adaptée à la pénétration du blindage ? Ou peut-être que l'essentiel est que les données de V. L. Kofman sont des valeurs calculées, mais en pratique, les obus britanniques obtiendraient-ils un meilleur résultat ?
Eh bien, nous avons à notre disposition des données sur les résultats du bombardement du cuirassé "Baden"

Ainsi, l'un des obus britanniques, frappant à un angle de 18 degrés. à une vitesse de 472 m / s., "maîtrisé" le blindage frontal de 350 mm de la tourelle allemande de calibre principal. Ces données sont d'autant plus précieuses que dans ce cas, ce ne sont pas les blindés britanniques, mais allemands qui ont subi des bombardements, c'est-à-dire que les tests des canons 381-mm/42 et 380-mm/45 sont donc dans un seul système de coordonnées..
Hélas, ils ne nous aident pas trop. Si nous supposons que l'obus anglais a percé la tour allemande, comme on dit, "avec le dernier peu de force", et s'il y avait eu un blindage de 351 mm, il aurait échoué, alors son (K) serait égal à 2021. Il est intéressant, en passant, que S. Vinogradov déclare que le projectile britannique, qui a pénétré le blindage frontal de 350 mm de la tour allemande, n'a pas été retrouvé par la suite, mais en fait le rapport indique autre chose - il a explosé, et il y a un description de l'endroit où les fragments ont volé dans la tour.
Bien sûr, nous n'avons aucune raison absolue de supposer que cette pénétration était la limite pour un projectile de 381 mm, ou même proche de cela. Mais néanmoins, selon certains signes indirects, on peut supposer que c'était exactement le cas. Un autre coup "fait allusion" à cela: un projectile britannique de 871 kg frappant un barbet de 350 mm à un angle de 11 degrés, bien qu'il ait pu faire un trou dans le blindage d'un diamètre de 40 cm, il n'a pas pénétré à l'intérieur du barbet lui-même, éclatant en train de surmonter l'armure. Dans ce cas, le coup s'est produit presque au centre même du barbet, c'est-à-dire la courbure de la plaque de blindage, si cela avait une influence, c'était le minimum.
De tout ce qui précède, on peut essayer de tirer quelques conclusions, mais, en raison de la fragilité de la base de preuves, elles seront bien sûr de nature très conjecturale.
Conclusion 1: les blindés allemands pendant la Première Guerre mondiale ont à peu près égalé les Britanniques en termes de durabilité. Cette conclusion est valable si la déclaration de V. L. Kofman que le canon britannique de 381 mm/42 était capable de pénétrer un blindage égal à son calibre de 70 kbt, et si l'on ne s'est pas trompé en supposant que la pénétration de 350 mm de la plaque frontale de la tourelle allemande sous un angle de 18 degrés et une vitesse de 472 m/s… est la limite ou très proche de la limite de pénétration du projectile britannique de 381 mm.
Conclusion 2e. Apparemment, la forme et la qualité du projectile allemand de 380 mm lui procuraient une meilleure pénétration du blindage que le projectile anglais. Sur la base des données ci-dessus, nous pouvons supposer que le coefficient (K) du projectile britannique de 381 mm lors du tir sur des blindés allemands était d'environ 2 000, tandis que le projectile allemand de 380 mm était d'environ 1 900. Si notre premier est correct, la conclusion que le la résistance de blindage des blindés britanniques et allemands est approximativement équivalente, il est évident que la seule raison du coefficient inférieur (K) ne peut être que le projectile lui-même.
Pourquoi un obus allemand pourrait-il être meilleur ? Son calibre est légèrement plus petit, d'un millimètre, mais, bien sûr, cela pourrait difficilement avoir un effet significatif. Le calcul montre qu'avec la même masse (750 kg), un changement de calibre de 1 millimètre entraînera une augmentation de la pénétration du blindage de 1,03 millimètre. Le projectile allemand est également plus court - sa longueur était de calibre 3,5, tandis que la longueur du "Greenboy" britannique est de calibre 4. Il y a peut-être eu d'autres différences aussi. Bien entendu, la qualité de l'acier à partir duquel le projectile est fabriqué joue ici un rôle important.
Calculons maintenant la pénétration du blindage des canons allemands et britanniques sur une distance de 75 câbles - une distance généralement acceptée pour une bataille décisive, où l'on pouvait s'attendre à suffisamment de coups pour détruire un navire ennemi de la ligne.
À la distance indiquée, 871 kg d'un obus de canon britannique de 381 mm / 42, tiré à une vitesse initiale de 752 m / s, ont touché la plaque de blindage positionnée verticalement à un angle de 13,05 degrés et sa vitesse "sur la plaque" était de 479,6 m / s … Avec (K) égal à 2 000, selon la formule de Jacob de Marr, la pénétration du blindage du projectile britannique était de 376, 2 mm.
Quant à l'obus allemand, tout est un peu plus compliqué. Si notre conclusion selon laquelle il surpassait l'anglais en termes de pénétration de blindage est correcte, alors les capacités du canon allemand 380-mm/45 sur 75 câbles étaient très proches du canon anglais de quinze pouces. À cette distance, le projectile allemand de 750 kg a touché la cible à un angle de 12,42 degrés à une vitesse de 482,2 m / s, et à (K) égal à 1 900, la pénétration du blindage était de 368,9 mm. Mais si l'auteur de cet article se trompe encore et que pour le canon allemand il vaut la peine d'utiliser le même coefficient que pour le canon anglais, alors les capacités du projectile de 380 mm tombent à 342,9 mm.
Néanmoins, selon l'auteur, la pénétration du blindage du projectile allemand est la plus proche de 368, 9 mm (après tout, le tir pratique a donné un coefficient de 1 913, malgré le fait que le projectile volait alors à 2,5 km), mais la pénétration du blindage du projectile anglais peut être légèrement inférieur calculé. En général, on peut considérer qu'à une distance de 75 câbles, les systèmes d'artillerie britannique et allemand sont assez comparables en termes de pénétration de blindage.
Mais avec le canon américain 356 mm/45, tout s'est avéré beaucoup plus intéressant. Les données précédemment citées pour les obus pesant 680 kg doivent être considérées comme canoniques dans la littérature en langue russe.
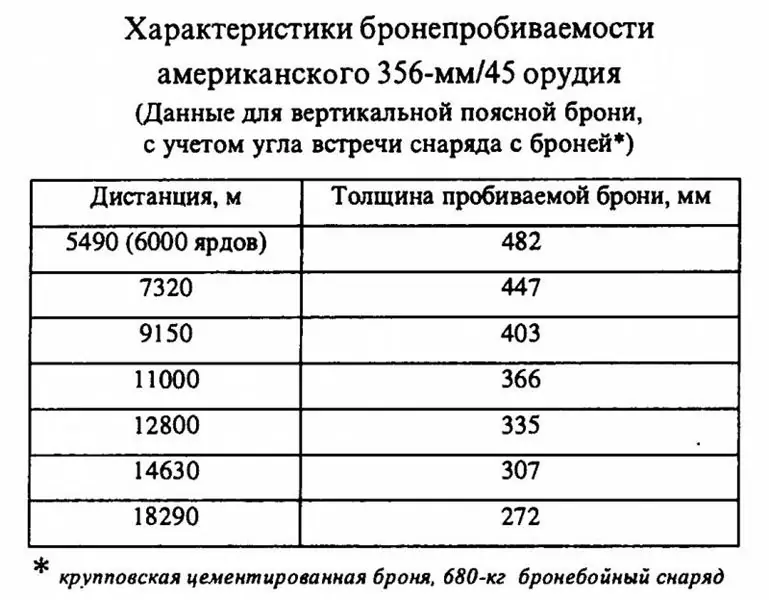
En fait, les valeurs qui y sont indiquées semblent conduire à des conclusions tout à fait évidentes: si même les obus de 680 kg apparus aux États-Unis après 1923 sont inférieurs en pénétration de blindage à leurs 380-381 mm européens " collègues", alors de quoi parler vraiment les premiers obus de 635 kg, qui étaient équipés d'artillerie de 356 mm de dreadnoughts américains ! Ils sont plus légers, ce qui signifie qu'ils perdent de la vitesse plus rapidement en vol, alors que leur vitesse initiale ne dépassait pas les obus plus lourds, et en termes de forme et de qualité, les munitions de 1923 devraient avoir un avantage. Il est clair comme le jour que les "Pennsylvania" américains au moment de leur entrée en service étaient inférieurs en termes de pénétration de blindage aux dreadnoughts britanniques et allemands. Eh bien, c'est évident, n'est-ce pas?
C'est exactement la conclusion qu'a tirée l'auteur, compte tenu des capacités des canons américains de quatorze pouces dans l'article Cuirassés "Standard" des États-Unis, de l'Allemagne et de l'Angleterre. "Pennsylvanie" américaine ". Et puis il a pris une calculatrice …
Le fait est que le calcul selon la formule de Marra montrait que les canons américains de 356 mm/45 avaient la pénétration de blindage indiquée dans le tableau avec un coefficient (K) égal à 2 317 ! En d'autres termes, les projectiles américains de 680 kg présentés dans le tableau ont montré des résultats lorsqu'ils ont été exposés à un blindage qui n'a pas été créé à l'époque de la Première Guerre mondiale, mais sur des échantillons beaucoup plus tardifs et plus durables.
Il est difficile de dire à quel point la force de la protection blindée a augmenté dans l'intervalle entre la première et la seconde guerre mondiale. Dans les sources en langue russe, il n'y a que des références brèves et souvent contradictoires à cette question, sur la base desquelles on peut supposer que la résistance de l'armure de Krupp a augmenté d'environ 20 à 25 %. Ainsi, pour les obus de gros calibre de l'ère du Premier Monde, la croissance du coefficient (K) passera de 1 900 - 2 000 à 2 280 - 2 500, mais il faut ici se rappeler qu'avec une augmentation de la qualité de la protection du blindage, bien sûr, la qualité des obus a également augmenté, et donc pour les munitions lourdes de la Seconde Guerre mondiale (K) peut-être moins. Par conséquent, (K) d'un montant de 2 317 pour les obus d'après-guerre, naturellement améliorés compte tenu de l'expérience acquise précédemment, semble assez organique, mais pour les armures de l'époque de la Seconde Guerre mondiale, pas la première.
Mais en fixant le coefficient (K) des obus américains de 680 kg au niveau de 2 000, c'est-à-dire en ramenant la qualité de la protection blindée à l'époque de la Première Guerre mondiale, pour une distance de 75 câbles on obtiendra un blindage pénétration au niveau de 393,5 mm, c'est-à-dire supérieure à celle des canons de quinze pouces britanniques et allemands !

La conversion en projectile de 635 kg donne une correction très insignifiante - le calculateur balistique a montré qu'à une distance de 75 câbles, ayant un angle d'incidence de 10, 82 degrés. et la vitesse "sur le blindage" 533, 2 m à (K) égal à 2 000, le projectile américain pénètre le blindage de l'époque de la Première Guerre mondiale, 380 mm d'épaisseur, c'est-à-dire nettement plus que son propre calibre !
En revanche, il est fort possible qu'un tel calcul ne soit toujours pas tout à fait correct. Le fait est que, selon certains rapports, le coefficient (K) pour le même blindage diminue avec une augmentation du calibre du projectile. Ainsi, par exemple, dans nos calculs, la valeur maximale (K) pour le système d'artillerie allemand 380-mm / 45, obtenue par calcul et publiée dans les sources, est de 2 083. Dans le même temps, les calculs pour le 305-mm allemand / 50 canons, qui ont été installés sur les navires de la Kaiserlichmarine en commençant par les Helgolands, les données des sources sur la pénétration du blindage donnent (K) au niveau de 2 145. En conséquence, il est possible que les canons de 356 mm / 45 (K) = 2 000 nous avons pris pour calculer que la pénétration du blindage des canons américains est encore trop faible.
De plus, malheureusement, l'auteur n'a pas "d'indices" pour comparer la résistance du blindage du blindage américain Krupp avec ses homologues européens. Il ne reste plus qu'à la considérer comme équivalente à la protection blindée allemande et anglaise, bien que ce ne soit bien sûr pas le cas.
Résumons toutes ces données plutôt chaotiques. Compte tenu des erreurs des « méthodes » utilisées dans les calculs, on peut supposer avec un degré de probabilité élevé que La pénétration de blindage de la protection de blindage verticale des canons de calibre principal des cuirassés Rivenge, Bayern et Pennsylvania à une distance de 75 câbles était approximativement la même et était d'environ 365-380 mm.
Malgré un tas d'hypothèses, les données dont nous disposons nous permettent tout de même de tirer quelques conclusions concernant la protection des blindages verticaux. Mais avec le franchissement des barrières horizontales, qui sont des ponts blindés, tout est beaucoup plus compliqué. Le fait est que Jacob de Marr, malheureusement, ne s'est pas du tout soucié de créer une formule pour déterminer la force de la défense horizontale. Sa formule de base, adaptée aux types d'armures modernes, ne convient qu'au calcul d'armures cimentées d'une épaisseur supérieure à 75 mm. Cette formule est donnée dans l'annexe n° 1 de cet article, et tous les calculs précédents de l'article ont été effectués à partir de celle-ci.
Mais les ponts des navires de ces années-là n'étaient pas protégés par un blindage cimenté (hétérogène) mais par un blindage homogène, auquel manquait une couche durcie en surface. Pour de telles armures (mais - installées verticalement !), une formule différente est utilisée, destinée à évaluer des plaques de blindage non cimentées d'une épaisseur inférieure à 75 mm, elle est donnée en annexe n°2.
Je voudrais noter que ces deux formules sont tirées d'une source plus que sérieuse: « Le cours de la tactique navale. Artillerie et armure 1932, auteur - Professeur de l'Académie navale RKKA L. G. Goncharov, l'un des principaux experts de l'URSS d'avant-guerre dans le domaine de l'artillerie navale.
Et hélas, aucune d'entre elles n'est adaptée pour évaluer la durabilité d'une protection horizontale. Si nous utilisons la formule pour un blindage cimenté, alors à une distance de 75 câbles, nous obtenons une faible pénétration du blindage: 46,6 mm pour 381 mm / 42 britannique, 39,5 mm pour 380 mm / 45 allemand et 33,8 mm pour 356 mm / 45 américain armes à feu. Si nous utilisons la deuxième formule pour un blindage non cimenté, nous obtenons que lorsqu'ils sont touchés à un angle typique sur une distance de 75 câbles, les trois systèmes d'artillerie pénètrent facilement dans une plaque de blindage de 74 mm, après quoi ils conservent une énorme quantité d'énergie cinétique - par exemple, l'anglais 381- mm, un projectile destiné à pénétrer un blindage de cette épaisseur à une distance de 75 câbles aura une vitesse de 264,5 m/s, alors que sa vitesse sera de 482,2 m/s. Si l'on ignore la limitation de l'épaisseur de la plaque de blindage, il s'avère que le projectile britannique de 381 mm, selon la formule ci-dessus, est capable de pénétrer un blindage de pont d'une épaisseur supérieure à 180 mm ! Ce qui, bien sûr, est totalement impossible.
Si nous essayons de nous référer aux résultats des tests du cuirassé de la classe Bayern, nous verrons que les obus britanniques perforants de 871 kg ont frappé à deux reprises le blindage horizontal des tours, qui avait une épaisseur de 100 mm sous un angle de 11 degrés., ce qui correspond à une distance de 67,5 câbles pour un projectile avec une vitesse initiale de 752 m/s et 65 câbles - pour un projectile avec une vitesse initiale de 732 m/s. Les deux fois, l'armure n'était pas percée. Mais dans un cas, le projectile, en ricochant, a fait une rainure dans l'armure d'une profondeur de 70 cm, c'est-à-dire que la plaque était très fortement pliée. Et dans le second, bien que l'obus, encore une fois, ait ricoché, l'armure était non seulement concave de 10 cm, mais également déchirée.

La nature similaire des dommages suggère que, bien que le blindage allemand de 100 mm assurait une protection aux distances indiquées, il était, sinon à la limite du possible, alors très proche de cela. Mais le calcul selon la formule du blindage cimenté donne une pénétration du blindage de seulement 46,6 mm à une distance plus grande, où l'angle d'incidence sera plus élevé, et, par conséquent, il serait plus facile pour le projectile de pénétrer dans le blindage du pont. Autrement dit, selon la formule, il s'avère que le pont de 100 mm devrait refléter en plaisantant et avec une grande marge de sécurité des obus anglais - cependant, la pratique ne le confirme pas. Dans le même temps, selon des calculs utilisant la formule des blindages non cimentés, il s'avère que les toits du calibre principal de Baden auraient dû être facilement percés, et - avec une grande quantité d'énergie d'obus - ce qui, encore une fois, n'est pas du tout confirmé par la pratique.
Je dois dire que de telles inexactitudes dans les calculs ont une explication tout à fait logique. Comme nous l'avons dit plus tôt, les formules de de Marr ne sont pas une description mathématique des processus physiques, mais sont juste une fixation des modèles obtenus lors des tests d'armure. Mais une protection de blindage verticale, et non horizontale, a été testée, et il n'est pas du tout surprenant que les motifs dans ce cas cessent tout simplement de fonctionner: pour un blindage situé horizontalement, dans lequel les obus frappent à un très petit angle par rapport à leur surface, ces motifs, bien sûr, sont complètement différents.
L'auteur de cet article est tombé sur des opinions "sur Internet" selon lesquelles les formules de de Marr fonctionnent efficacement à des angles de déviation par rapport à la normale ne dépassant pas 60 degrés, c'est-à-dire de 30 degrés à la surface de la dalle et plus. On peut supposer que cette évaluation est très proche de la vérité.
Ainsi, force est de constater avec regret que l'appareil mathématique dont dispose l'auteur ne permet pas d'effectuer des calculs fiables de la résistance de protection horizontale des cuirassés Rivenge, Bayern et Pennsylvania. Compte tenu de ce qui précède, il sera difficile d'utiliser les données sur la pénétration du blindage du blindage horizontal fournies dans diverses sources - en règle générale, elles sont toutes basées sur les mêmes calculs selon les formules de de Marr et sont incorrectes.






